MATEMAQUI

Elementos da função

Função x², definida para { -3,-2,-1,0 }. Observar o conjunto domínio (D), contradomínio (CD) e imagem (delineado pela linha tracejada).

Seja

f: D \rightarrow CD

uma função. Toda função consta de três partes:

A primeira é o conjunto $D,$ chamado de domínio da função, é o conjunto onde a função é definida ⁵ , ou seja, ele contém todos os elementos x para os quais a função deve ser definida.
Outra parte integrante da função é o contradomínio (representado na figura por 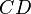$CD$ ), que é o conjunto que contém os elementos que podem ser relacionados a elementos do domínio. Em outras palavras, é o conjunto onde a função toma valores.⁵ Dentro do contradomínio, define-se o conjunto imagem como o conjunto de valores que efetivamente f(x) assume. O conjunto imagem é, pois, sempre um subconjunto do contradomínio.
A terceira parte de uma função é a regra que permite associar, de modo bem determinado, a cada elemento $x \in D,$ um único elemento $f(x) \in CD,$ chamado o valor que a função assume em x (ou no ponto x).⁵

A função, portanto, se caracteriza pelo domínio, o contradomínio, e pela lei de associação (regra). A função

f: \R \to \R, \ f(x) = x^2

é diferente da função

g: \R \to \R^{+}, \ g(x) = x^2,

pois o contradomínio é diferente.

Gráficos de função

Ver artigo principal: Gráfico#Gráficos de função

As funções são comumente representadas em gráficos. O gráfico de uma função f : D → I é o conjunto dos pares ordenados em D x I da forma ( x , f (x) ), ou seja:

\left\{\left(x,f(x)\right) : x \in D \right\}

ou equivalentemente:

\left\{\left(x,y\right)\in D\times I : x \in D \mbox{ e } y=f(x) \right\}

os termos deste par ordenado são chamados de abcissa e ordenada, respectivamente.
Uma função é determinada pelo seu gráfico e pela especificação do conjunto de chegada. Assim, se duas funções têm o mesmo gráfico, uma poderá ser sobrejectiva e a outra não. No entanto, a injectividade de uma função é completamente determinada pelo gráfico.

Tipos de funções

Dependendo do tipo de regra que associa os elementos do domínio aos elementos do contradomínio de uma função, ela pode receber nomes específicos. Por exemplo,

Se a regra que associa o domínio ao contradomínio é um polinômio, então a função é dita uma função polinomial. Exemplos de funções polinomiais são a função linear e a função quadrática.⁶
Se a regra eleva o logaritmo neperiano pelos elementos do domínio, então a função é dita exponencial.⁶

Os tipos de funções podem ser classificados de acordo com o seu comportamento com relação à regra uma única saída para cada entrada. Como não foi dito nada sobre as entradas, ou se as saídas tem que ser únicas temos que resolver estas ambiguidades. Ao fazer isto encontramos apenas três tipos de classes de funções, e classe é empregado aqui como classificação mesmo e não como classe de equivalência.⁶

Tipo de função	Característica da função	Conjunto imagem	Explicação visual	Exemplo

Integrante: Loruhama Batista Josino De Moura e Millena Hávilla Marinheiro Vidal

MATEMAQUI

segunda-feira, 2 de junho de 2014

Elementos da função

Gráficos de função

Tipos de funções

Nenhum comentário:

Postar um comentário