Função de 1º grau

Zero e Equação do 1º Grau

   Chama-se zero ou raiz da função polinomial do 1º grau f(x) = ax + b, a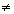0, o número real x tal que  f(x) = 0.

   Temos:

   f(x) = 0        ax + b = 0       

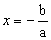
   Vejamos alguns exemplos:

1. Obtenção do zero da função f(x) = 2x - 5:
                                       f(x) = 0        2x - 5 = 0       
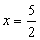
2. Cálculo da raiz da função g(x) = 3x + 6:
                                       g(x) = 0        3x + 6 = 0        x = -2
      
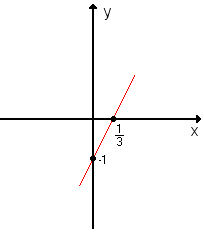
3. Cálculo da abscissa do ponto em que o gráfico de h(x) = -2x + 10 corta o eixo das abicissas:
   O ponto em que o gráfico corta o eixo dos x é aquele em que h(x) = 0; então:
       h(x) = 0        -2x + 10 = 0        x = 5

 

Crescimento e decrescimento

   Consideremos a função do 1º grau y = 3x - 1. Vamos atribuir valores cada vez maiores a x e observar o que ocorre com y:

x -3 -2 -1 0 1 2 3 y -10 -7 -4 -1 2 5 8       Notemos que, quando aumentos o valor de x, os correspondentes     valores de y também aumentam. Dizemos, então que a     função y = 3x - 1 é crescente.    Observamos novamente seu gráfico:

Regra geral:
a função do 1º grau f(x) = ax + b é crescente quando o coeficiente de x é positivo (a > 0);
a função do 1º grau f(x) = ax + b é decrescente quando o coeficiente de x é negativo (a < 0);
Justificativa:

• para a > 0: se x₁ < x₂, então ax₁ < ax₂. Daí, ax₁ + b < ax₂ + b, de onde vem f(x₁) < f(x₂).
• para a < 0: se x₁ < x₂, então ax₁ > ax₂. Daí, ax₁ + b > ax₂ + b, de onde vem f(x₁) > f(x₂).
  
  Integrante: Loruhama Batista Josino de Moura.