Integrante: Bruna Leandro Rodrigues.

 Função de 1º grau

Zero e Equação do 1º Grau

   Chama-se zero ou raiz da função polinomial do 1º grau f(x) = ax + b, a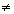0, o número real x tal que  f(x) = 0.

   Temos:

   f(x) = 0        ax + b = 0       

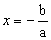
   Vejamos alguns exemplos:

1. Obtenção do zero da função f(x) = 2x - 5:
                                       f(x) = 0        2x - 5 = 0       
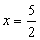
2. Cálculo da raiz da função g(x) = 3x + 6:
                                       g(x) = 0        3x + 6 = 0        x = -2
      
3. Cálculo da abscissa do ponto em que o gráfico de h(x) = -2x + 10 corta o eixo das abicissas:
   O ponto em que o gráfico corta o eixo dos x é aquele em que h(x) = 0; então:
       h(x) = 0        -2x + 10 = 0        x = 5

 

Crescimento e decrescimento

   Consideremos a função do 1º grau y = 3x - 1. Vamos atribuir valores cada vez maiores a x e observar o que ocorre com y:

x -3 -2 -1 0 1 2 3 y -10 -7 -4 -1 2 5 8       Notemos que, quando aumentos o valor de x, os correspondentes     valores de y também aumentam. Dizemos, então que a     função y = 3x - 1 é crescente.    Observamos novamente seu gráfico:

Regra geral:
a função do 1º grau f(x) = ax + b é crescente quando o coeficiente de x é positivo (a > 0);
a função do 1º grau f(x) = ax + b é decrescente quando o coeficiente de x é negativo (a < 0);
Justificativa:

• para a > 0: se x₁ < x₂, então ax₁ < ax₂. Daí, ax₁ + b < ax₂ + b, de onde vem f(x₁) < f(x₂).
• para a < 0: se x₁ < x₂, então ax₁ > ax₂. Daí, ax₁ + b > ax₂ + b, de onde vem f(x₁) > f(x₂).
  
  Integrante: Loruhama Batista Josino de Moura.

Gráfico de uma função do 1° grau.

O estudo das funções é importante, uma vez que elas podem ser aplicadas em diferentes circunstâncias: nas engenharias, no cálculo estatístico de animais em extinção, etc.
O significado de função é intrínseco à matemática, permanecendo o mesmo para qualquer tipo de função, seja ela do 1° ou do 2° grau, ou uma função exponencial ou logarítmica. Portanto, a função é utilizada para relacionar valores numéricos de uma determinada expressão algébrica de acordo com cada valor que a variável x assume.
Sendo assim, a função do 1° grau relacionará os valores numéricos obtidos de expressões algébricas do tipo (ax + b), constituindo, assim, a função f(x) = ax + b.
Note que para definir a função do 1° grau, basta haver uma expressão algébrica do 1° grau. Como dito anteriormente, o objetivo da função é relacionar para cada valor de x um valor para o f(x). Vejamos um exemplo para a função f(x)= x – 2.
x = 1, temos que f(1) = 1 – 2 = –1
x = 4, temos que f(4) = 4 – 2 = 2
Note que os valores numéricos mudam conforme o valor de x é alterado, sendo assim obtemos diversos pares ordenados, constituídos da seguinte maneira: (x, f(x)). Veja que para cada coordenada x, iremos obter uma coordenada f(x). Isso auxilia na construção de gráficos das funções.
Portanto, para que o estudo das funções do 1° grau seja realizado com sucesso, compreenda bem a construção de um gráfico e a manipulação algébrica das incógnitas e dos coeficientes.
Integrante: Bruna Leandro Rodrigues.

Criado por René Descartes, o plano cartesiano consiste em dois eixos perpendiculares, sendo o horizontal chamado de eixo das abscissas e o vertical de eixo das ordenadas. O plano cartesiano foi desenvolvido por Descartes no intuito de localizar pontos num determinado espaço. As disposições dos eixos no plano formam quatro quadrantes, mostrados na figura a seguir:

O encontro dos eixos é chamado de origem. Cada ponto do plano cartesiano é formado por um par ordenado (x , y ), onde x: abscissa e y: ordenada.

Marcando pontos no plano cartesiano

Dados os pontos A(3,6), B(2,3), C(-1,2), D(-5,-3), E(2,-4), F(3,0), G(0,5), represente-os no plano cartesiano.

Marcando o ponto A(3,6)
Primeiro: localiza-se o ponto 3 no eixo das abscissas
Segundo: localiza-se o ponto 6 no eixo das ordenadas
Terceiro: Traçar a reta perpendicular aos eixos, o encontro delas será o local do ponto.



O sistema de coordenadas cartesianas possui inúmeras aplicações, desde a construção de um simples gráfico até os trabalhos relacionados à cartografia, localizações geográficas, pontos estratégicos de bases militares, localizações no espaço aéreo, terrestre e marítimo.

Integrante: Loruhama Batista Josino de Moura

Elementos da função

Ver artigo principal: Conjunto imagem

Função x², definida para { -3,-2,-1,0 }. Observar o conjunto domínio (D), contradomínio (CD) e imagem (delineado pela linha tracejada).

Seja uma função. Toda função consta de três partes:

• A primeira é o conjunto chamado de domínio da função, é o conjunto onde a função é definida ⁵ , ou seja, ele contém todos os elementos x para os quais a função deve ser definida.
• Outra parte integrante da função é o contradomínio (representado na figura por 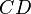), que é o conjunto que contém os elementos que podem ser relacionados a elementos do domínio. Em outras palavras, é o conjunto onde a função toma valores.⁵ Dentro do contradomínio, define-se o conjunto imagem como o conjunto de valores que efetivamente f(x) assume. O conjunto imagem é, pois, sempre um subconjunto do contradomínio.
• A terceira parte de uma função é a regra que permite associar, de modo bem determinado, a cada elemento um único elemento chamado o valor que a função assume em x (ou no ponto x).⁵

A função, portanto, se caracteriza pelo domínio, o contradomínio, e pela lei de associação (regra). A função é diferente da função pois o contradomínio é diferente.

Gráficos de função

Ver artigo principal: Gráfico#Gráficos de função

As funções são comumente representadas em gráficos. O gráfico de uma função f : D → I é o conjunto dos pares ordenados em D x I da forma ( x , f (x) ), ou seja:

ou equivalentemente:

os termos deste par ordenado são chamados de abcissa e ordenada, respectivamente.
Uma função é determinada pelo seu gráfico e pela especificação do conjunto de chegada. Assim, se duas funções têm o mesmo gráfico, uma poderá ser sobrejectiva e a outra não. No entanto, a injectividade de uma função é completamente determinada pelo gráfico.

Tipos de funções

Dependendo do tipo de regra que associa os elementos do domínio aos elementos do contradomínio de uma função, ela pode receber nomes específicos. Por exemplo,

• Se a regra que associa o domínio ao contradomínio é um polinômio, então a função é dita uma função polinomial. Exemplos de funções polinomiais são a função linear e a função quadrática.⁶
• Se a regra eleva o logaritmo neperiano pelos elementos do domínio, então a função é dita exponencial.⁶

Os tipos de funções podem ser classificados de acordo com o seu comportamento com relação à regra uma única saída para cada entrada. Como não foi dito nada sobre as entradas, ou se as saídas tem que ser únicas temos que resolver estas ambiguidades. Ao fazer isto encontramos apenas três tipos de classes de funções, e classe é empregado aqui como classificação mesmo e não como classe de equivalência.⁶

Tipo de função	Característica da função	Conjunto imagem	Explicação visual	Exemplo

Integrante: Loruhama Batista Josino De Moura e Millena Hávilla Marinheiro Vidal

 Função de 1º grau

  Definição
 Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados e a0.
 Na função f(x) = ax + b, o número a é chamado de coeficiente de x e o número b é chamado termo constante.
 Veja alguns exemplos de funções polinomiais do 1º grau:
 f(x) = 5x - 3, onde a = 5 e b = - 3
 f(x) = -2x - 7, onde a = -2 e b = - 7
 f(x) = 11x, onde a = 11 e b = 0
Gráfico
    O gráfico de uma função polinomial do 1º grau,  y = ax + b, com a0, é uma reta oblíqua aos eixos Ox e Oy.
    Exemplo:
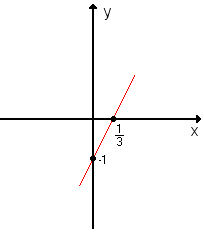
    Vamos construir o gráfico da função y = 3x - 1:
    Como o gráfico é uma reta, basta obter dois de seus pontos e ligá-los com o auxílio de uma régua:
    a)    Para   x = 0, temos   y = 3 · 0 - 1 = -1; portanto, um ponto é (0, -1).
    b)    Para   y = 0, temos   0 = 3x - 1; portanto, e outro ponto é .
    Marcamos os pontos (0, -1) e no plano cartesiano e ligamos os dois com uma reta.

x y 0 -1 0

    Já vimos que o gráfico da função afim y = ax + b é uma reta.
    O coeficiente de x, a, é chamado coeficiente angular da reta e, como veremos adiante, a está ligado à inclinação da reta em relação ao eixo Ox.

    O termo constante, b, é chamado coeficiente linear da reta. Para x = 0, temos y = a · 0 + b = b. Assim, o coeficiente linear é a ordenada do ponto em que a reta corta o eixo Oy.
,
Integrante: MIllena Hávilla Marinheiro Vidal
 

Representação de Pontos no Plano Cartesiano

A representação de pontos neste plano é feita através de pares ordenados, onde o primeiro número se refere à abscissa e o segundo a ordenada.

O ponto P₁(3, 2) tem abscissa 3 e ordenada 2, no qual o símbolo (3, 2) representa um par ordenado. O ponto P₂(2, 3) tem abscissa 2 e ordenada 3. É importante frisarmos que os pontos P₁ e P₂ são pontos distintos, pois em um par ordenado a ordem dos números é relevante.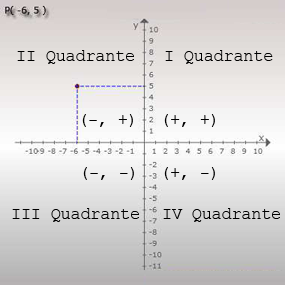
Dois pares ordenados (a, b) e (c, d) são iguais se e somente se a = c e b = d.
Na figura ao lado vemos a representação do ponto P(-6, 5).
Ao ponto localizado no cruzamento de ambos os eixos damos o nome de origem do sistema de coordenadas cartesianas, representado por O(0, 0).

Quadrantes do Plano Cartesiano

Vemos nesta figura que o eixo x e o eixo y dividem o plano em quatro regiões. A região do canto superior direito é o primeiro quadrante, a região à sua esquerda, do outro lado do eixo y é o segundo quadrante. Abaixo deste temos o terceiro quadrante e à sua direita, ou seja, abaixo do primeiro temos o quarto quadrante.

Os quadrantes são dispostos em sentido anti-horário.

Sinal da Abscissa e da Ordenada de um Ponto

Todos os pontos no primeiro quadrante possuem abscissa e ordenada positivas. Exemplo: P₁(3, 5).

No segundo quadrantes todos os pontos possuem abscissa negativa e ordenada positiva. Exemplo: P₂(-4, 2).
Todos os pontos no terceiro quadrante possuem abscissa e ordenada negativas. Exemplo: P₃(-7, -1).
No quarto quadrante todos os pontos possuem abscissa positiva e ordenada negativa. Exemplo: P₂(8, -3).
Integrante: Adriane Cândido Monte